4.1 Импульс материальной точки массой m, движущийся со скоростью υ: p = mυ.

    4.2 Импульс системы тел: p = p₁ + p₂ + ... .

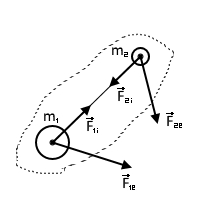
    4.3 Закон изменения и сохранения импульса. Рассмотрим пример системы двух тел (материальных точек) массами m₁ и m₂

    На эти тела действуют внутрение силы F_1i и F_2i, подчиненные третьему закону Ньютона, и внешние силы F_1e и F_2e.

    Импульс системы двух тел: p = p₁ + p₂, его изменение за время Δt: Δp = Δp₁ + Δp₂.

    Для каждого из двух тела по отдельности, согласно второму закону Ньютона, в ИСО:

        Δp₁ = F_1iΔt + F_1eΔt,

        Δp₂ = F_2iΔt + F_2eΔt.

С учетом третьего закона Ньютона получаем в ИСО

        Δp = F_1iΔt + F_2eΔt.

    Этот же результат справедлив для системы из произвольного числа материальных точек, а значит, и для любой системы тел.

    В ИСО изменение импульса системы тел равно сумме импульсов внешних сил, приложенных к этим телам.

    В ИСО импульс системы тел сохраняется, если сумма внешних сил, приложенных к телам системы, равна нулю.

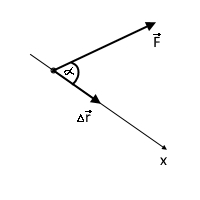    4.4 Работа силы: на малом перемещении, когда силу можно считать постоянной,

        A = |F| · |Δr| · cosα = F_x · Δx.

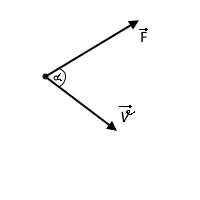
    4.5 Мощность силы: P = ΔA / Δt = F · υ · cosα.

    4.6 Кинетическая энергия материальной точки: E_к = mυ² / 2 = p² / (2m).

    Закон изменения кинетической энергии системы материальных точек. Для иллюстрации рассмотрим случай прямолинейного движения материальной точки по оси X. Согласно второму закону Ньютона в ИСО:

        ma_x = F_x, т. е. mΔυ_x = F_xΔt при Δt > 0.

    Умножим это равенство на υ_x: mυ_x · Δυ_x = F_x · (υ_xΔt) = F_xΔx = ΔA, где ΔA - элементарная работа (работа на бесконечно малом перемещении Δx, совершаемая за бесконечно малое время Δt).

    За малое время Δt > 0 величина Δυ_x > 0, поэтому изменение квадрата скорости за время Δt > 0 составляет

        Δ(υ_x²) = υ_x²(t + Δt) - υ_x²(t) = (υ_x + Δυ_x)² - υ_x² = (2υ_x + Δυ_x) · Δυ_x ≈ 2υ_x · Δυ_x.

    Таким образом, за бесконечно малое время Δt для материальной точки в ИСО в случае движения по прямой получаем Δ(mυ_x² / 2) = ΔA.

    Отсюда следует, что в случае трехмерного движения материальной точки в ИСО: Δ(mυ² / 2) = ΔA, т. е. ΔE_к = ΔA.

    Рассматривая конечный интервал времени τ, считаем его суммой бесконечно малых интервалов Δt, на каждом из которых справедливо полученное равенство. Суммируя по отдельности левые и правые части таких равенств, приходим к результату: в ИСО изменение кинетической энергии материальной точки равно суммарной работе всех приложенных к телу сил (или, что то же самое, равно работе равнодействующей приложенных к телу сил): ΔE_к = ΔA.

    Переходя от одной материальной точки к их системе, определим кинетическую энергию такой системы как сумму кинетических энергий отдельных материальных точек:

        E_к = E_1к + E_2к + E_3к + ... = m₁υ₁² / 2 + m₂υ₂² / 2 + m₃υ₃² / 2 + ... .

    Для каждой очередной точки (с индексом i) в ИСО выполняется равенство ΔE_iк = A_i, т. е. изменение кинетической энергии каждой материальной точки равно работе всех сил, приложеных к этой точке. Поэтому для системы материальных точек в ИСО получаем

        ΔE_к = ΔE_1к + ΔE_2к + ΔE_3к + ... = A₁ + A₂ + A₃ + ... = A,

т. е. в ИСО изменение кинетической энергии ΔE_к системы материальных точек равно работе A всех сил, приложенных ко всем телам системы. Это значит, что учитывается работа всех внутренних сил и всех внешних сил, всех потенциальных сил (см. ниже) и всех непотенциальных сил.

    4.7 Введем понятие потенциальной силы: если при движении тела из произвольной точки 1 в произвольную точку 2 по любой траектории (на рисунке как пример показаны две траектории Ⅰ и Ⅱ) работа силы F, приложенных к телу, одна и та же, то сила F потенциальна.

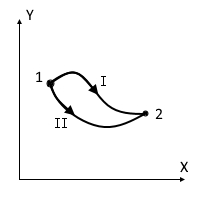    Равносильное определение: сила F потенциальна, если её работа по любой замкнутой траектории равна нулю.

    Пусть сила F потенциальна. Тогда ее работа А₁₂ зависит от точек 1 и 2, но не зависит от выбора траектории перехода из точки 1 в точку 2. В этом случае работу А₁₂ можно записать в виде разности значений потенциальной энергии E_п, заданной в каждой точке пространства, в том числе и в точках 1 и 2: А₁₂ = E_1п - E_2п = - ΔE_п.

    Таким образом, потенциальная энергия вводится как величина, изменение которой при переходе тела из одной точки в другую равно (с учетом знака) работе потенциальной силы при этом переходе.

    Из изучаемых в школьном курсе физики к потенциальным относятся гравитационные силы, силы упругости и силы электростатического воздействия на заряженные тела. В каждом из этих случаев известно выражение для потенциальной энергия тела, находящегося под воздействием этих сил.

    Потенциальная энергия тела массой m, находящегося в однородном поле тяжести на высоте h над началом отсчета: E_п = mgh.

    Потенциальная энергия деформированной пружины при ее удлинение или сжатии, равном x: E_п = kx² / 2.

    4.8 Закон изменения и сохранения механической энергии. В ИСО изменение кинетической энергии ΔE_к системы материальных точек равно работе А всех сил, приложенных к всем телам системы: ΔE_к = А. Каждую силу из числа действующих на тела системы относим либо к потенциальным, либо к непотенциальным. Тогда

        A = A_{всех потенциальных сил} + A_{всех непотенциальных сил}.

    Работа потенциальных сил представим через изменение потенциальной энергии системы материальных точек: A_{всех потенциальных сил} = - ΔE_п.

    Учтем, что механическая энергия системы тел E_м = E_к + E_п. Тогда

        ΔE_м = ΔE_к + ΔE_п = А - A_{всех потенциальных сил} = A_{всех непотенциальных сил}

    Таким образом, в ИСО для системы материальных точек (системы тел) изменение механической энергии равно работе всех непотенциальных сил, как внутренних, так и внешних: в ИСО ΔE_м = A_{всех непотенциальных сил}.

    Поэтому в ИСО механическая энергия системы материальных точек (системы тел) сохраняется, если работа всех непотенциальных сил, как внутренних, так и внешних, равна нулю: в ИСО ΔE_м = 0, если A_{всех непотенциальных сил} = 0.