3.1 Момент силы относительно оси вращения: M = Fl, где l - плечо силы F относительно оси вращения, проходящей через точку O перпендикулярно плоскости рисунка.

    3.2 Условия равновесия твердого тела в ИСО. Любое движение твердого тела сводится к суперпозиции поступательного и вращательного движений. Поэтому должны быть выполнены совместно два условия.

    Условия равновесия в ИСО относительно поступательного движения: F₁ + F₂ + ... = 0.

    Условия равновесия в ИСО относительно вращательного движения: M₁ + M₂ + ... = 0.

    В последнем равенстве нужно суммировать моменты сил, учитывая правило знаков: момент силы считается положительным, если под действием этой силы тело на оси выходит из состояния покоя, раскручиваясь против часовой стрелки.

    Теорема. Если сумма сил равна нулю, то сумма их моментов относительно двух параллельных друг другу осей одна и та же.

    В случае когда действуют силы произвольного направления, каждую силу можно представить в виде суммы составляющих, каждая из которых параллельна одной из координатных осей. Поэтому рассмотрим случай трех параллельных сил.

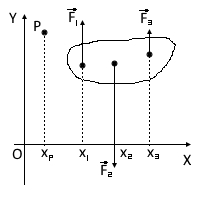    Пусть на тело действуют силы F₁, F₂ и F₃, параллельное оси OY, причём F_1y + F_2y + F_3y = 0. Через точку P проведём ось перпендикулярно плоскости рисунка. Сумма моментов сил F₁, F₂ и F₃ относительно этой оси

        M_P = F₁(x₁ - x_P) - F₂(x₂ - x_P) + F₃(x₃ - x_P) = F_1y(x₁ - x_P) + F_2y(x₂ - x_P) + F_3y(x₃ - x_P) = F_1yx₁ + F_2yx₂ + F_3yx₃ - x_P(F_1y + F_2y+ F_3y) = F_1yx₁ + F_2yx₂ + F_3yx₃ = M_O.

    Таким образом, сумма моментов сил F₁, F₂ и F₃ относительно оси, проходящей перпендикулярно плоскости XOY через точку P, равна сумме их моментов относительно параллельной оси, проходящей через начало координат, т. е. не зависит от выбора точки P. Теорема доказана.

    Мы получили право применять правило моментов не относительно реальной оси вращения (часто очевидно только ее направление, но не положение), а относительно любой параллельной ее оси. Но всё это возможно, только если сумма приложенных к телу сил равна нулю.

    3.3 Закон Паскаля: внешнее давление передается в покоящейся жидкости (покоящемся газе) по любому направлению без изменений. Это означает, во-первых, что давление в данной точке покоящейся жидкости (покоящегося газа) не зависит от ориентации площадки, на которой оно измеряется. Во-вторых, давление, измеренное в любой точке покоящейся жидкости, содержит слагаемое p₀ - внешнее давление над свободной поверхностью жидкости. Это проявляется в следующей формуле.

    3.4 Формула для давления в однородной жидкости плотностью ρ на глубине h в случае, когда жидкость и сосуд, куда она налита, покоятся относительно ИСО: p = p₀ + ρgh.

    3.5 Закон Архимеда. Если тело погружено в жидкость (газ) или они покоятся друг относительно друга, то на тело со стороны жидкости (газа) действует выталкивающая сила (сила Архимеда). Это сила точно такая же, как и та, которая действует на жидкость (газ) в объеме погруженной части тела. Поэтому по третьему закону Ньютона она равна по модулю и противоположна по направлению силе, с которой жидкость (газ) в объеме погруженной части тела действует на окружающую жидкость (газ), т. е. весу жидкости (газа) в объеме погруженной части тела: F_A = - P_Ж.

    Поскольку жидкость (газ) в объеме погруженной части тела покоятся, то сила Архимеда уравновешивает силу тяжести, действующую на жидкость (газ). Значит, сила Архимеда в ИСО приложена к центру тяжести жидкости (газа) в объеме погруженной части тела.

    Если тело и жидкость плотностью ρ покоятся друг относительно друга в ИСО, то

        F_A = P_Ж = m_Жg = ρgV_Ж.

    Если тело и жидкость плотностью ρ покоятся друг относительно друга, но движутся с ускорением a относительно ИСО, то

        F_A = P_Ж = m_Ж|g - a| = ρ|g - a|V_Ж.

    Отсюда видно, что при свободном падении (g = a) сила Архимеда равна нулю.

    Условия плавания тел

1. Тело и жидкость покоятся в ИСО. Тогда действующей на тело силы уравновешивают друг друга: F_T + F_A = 0, т. е. mg + m_Жg = 0, откуда mg = m_Жg, следовательно, m = m_Ж.
2. Тело и жидкость покоятся друг относительно друга, но движутся с ускорением a относительно ИСО. Тогда F_T + F_A = ma, т. е. mg + m_Ж(g - a) = ma. Следовательно, при g ≠ a в этом случае тоже m = m_Ж.